LANGTON'S ANT
Rules
Copy this magic link to share this set of rules with a friend
About
This page is a customizable implementation of Langton's Ant, a cellular automaton invented by Chris Langton in 1986. Langton's Ant is interesting because its very simple set of rules can lead to very complex emergent behavior. The simulation deals with computerized "ants" whose movements are controlled by a set of rules decided by the user. In its most basic form the simulation creates a single ant, which follows these rules:
- At a white square, turn 90° right, change the color of the square to black, then move forward one square
- At a black square, turn 90° left, change the color of the square to white, then move forward one square
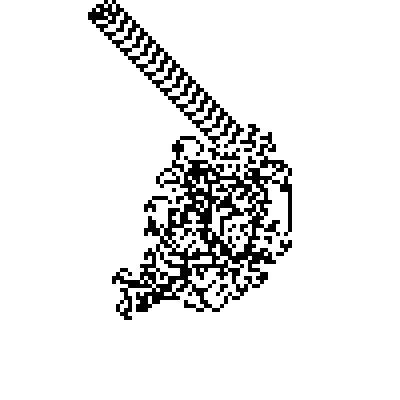
At first, the ant's movement appears to be essentially random, retracing its steps many times and turning in unpredictable ways. However, after about 10,000 iterations the ant begins moving in a pattern. It constructs a repeating "highway" in one direction, eventually reaching the edge of the grid. This is the really fascinating aspect of Langton's Ant: order arising out of chaos.
Extensions
The basic implementation of Langton's Ant is cool, but it does the same thing every time, which gets boring. Several ways to extend the functionality of the ant have been suggested over the years. For example, multiple ants can be simulated by pressing the "Add Ant" button, each with a unique starting position and direction. This can show how multiple ants interact with each other and give rise to different ordered patterns.

Another way to extend Langton's Ant is to add more colors, and more rules. By clicking the "Add Rule" button you can define any number of rules for the ants to obey. In addition to the basic "turn right" (R) and "turn left" (L), ants can also continue straight ahead (C) or turn 180° around (U).
The combination of these extensions can lead to some very interesting and unpredictable outcomes. Sometimes ordered patterns arise out of chaos, and sometimes symmetry and repetition degenerates into randomness. Unpredictable patterns often emerge from these simple rules.
The point of this page is to make it easy to experiment and play with different combinations of rules and ants. The next section explains how to use the provided options to do just that.
Limitations
You can't remove rules while the simulation is running. This is impossible because what should happen to an ant sitting on a square that is the color of a removed rule? You can change the color of rules while it's running, but this doesn't retroactively replace the old color. Instead, squares with the old color are just treated as if they were the new color.

Interesting Patterns
Here is an interesting configuration I found that repeats infinitely while occupying a finite amount of space.
This set of rules leads to several different patterns, including multiple spirals and highways (see image). Duplicating it four times leads to an even more interesting pattern, which repeats after 165,000 iterations.
Haskell Ant
I reimplemented Langton's Ant in the Haskell programming language for practice while I was learning that language. You can see that implementation and try it out for yourself at my GitHub. It's not as pretty or interactive as the web version, but it's way faster because it doesn't display every step along the way, only the final board after a given number of iterations.
Haskell Ant is configured through a command line interface, which can be hard to visualize. Instead, you can use the web version on this page to design an ant configuration and then just copy this conveniently auto-formatted command to try it in Haskell:
Just change the -n argument to specify a different number
of iterations to do before printing the result